Chapter 7 Linear Regressions, Quadratic Fits, Residuals, and Spatial
“How many data scientists does it take to change a light bulb? That depends. It is really a matter of power.”
This assignment combined several methods to look at relationships between crop yields and weather data over time.
Data from USDA National Agricultural Statistical Service (NASS). Assignment by Dr. Matthew Ross and Dr. Nathan Mueller of Colorado State University.
7.1 Weather Data Analysis
7.1.1 Load the PRISM daily maximum temperatures
# daily max temperature
# dimensions: counties x days x years
prism <- readMat("Data_sci_bookdown/data/prismiowa.mat")
# look at county #1
t_1981_c1 <- prism$tmaxdaily.iowa[1,,1] #first county, all days, first year
t_1981_c1[366] #check for leap year (366 days)## [1] NaNplot(1:366, t_1981_c1, type = "l") #base r plot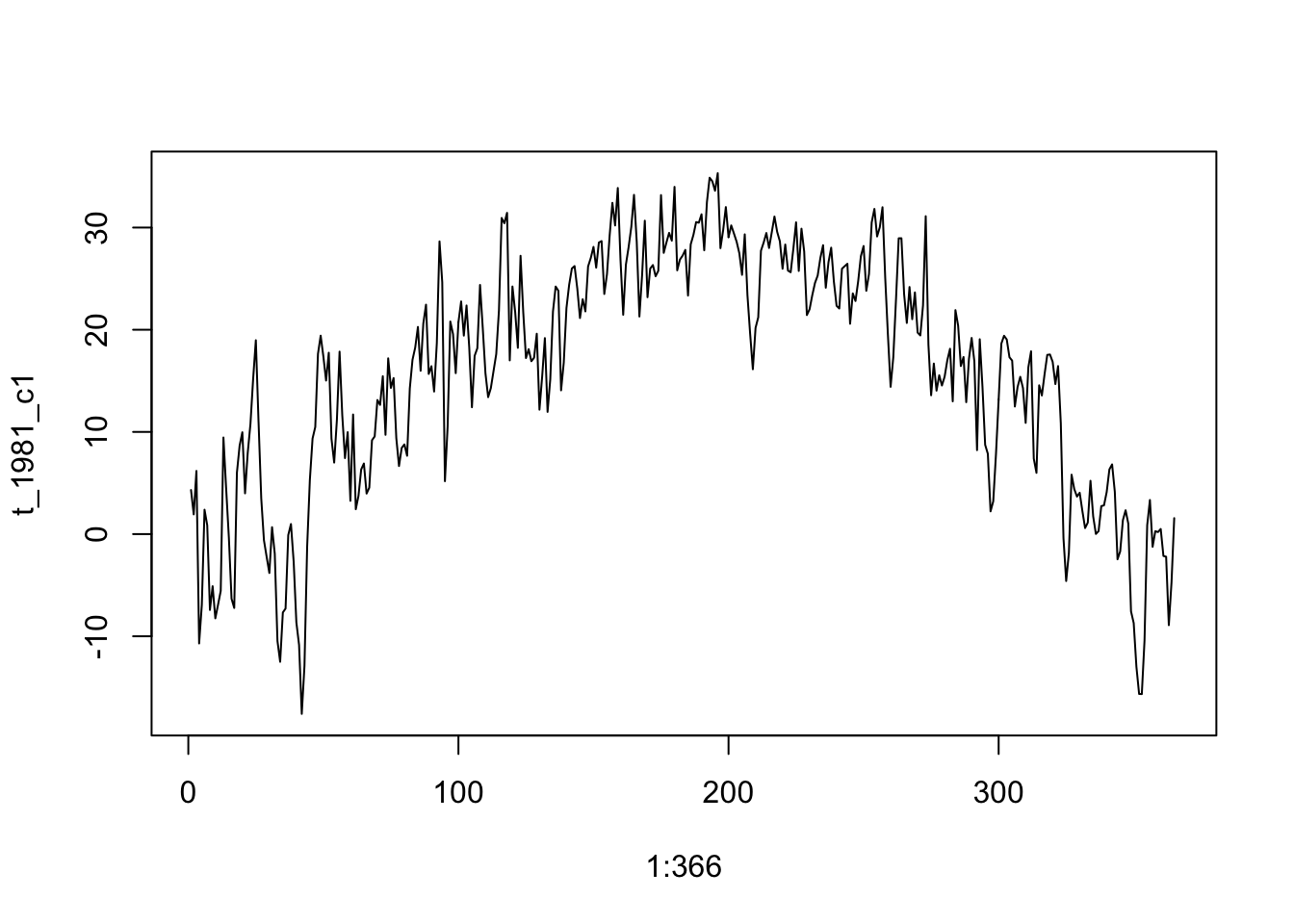
# assign dimension names to tmax matrix
dimnames(prism$tmaxdaily.iowa) <- list(prism$COUNTYFP, 1:366, prism$years) #add dimension names
# converted 3d matrix into a data frame
tmaxdf <- as.data.frame.table(prism$tmaxdaily.iowa)
# relabel the columns
colnames(tmaxdf) <- c("countyfp","doy","year","tmax") #name columns
tmaxdf <- tibble(tmaxdf) #tidyverse table7.1.2 Download NASS corn yield data
# set our API key with NASS
nassqs_auth(key = "B9113AF8-85C4-3CEE-8D93-6E885D49E24F") #Here put in API code from USDA QuickStats service
# parameters to query on
params <- list(commodity_desc = "CORN", util_practice_desc = "GRAIN", prodn_practice_desc = "ALL PRODUCTION PRACTICES", year__GE = 1981, state_alpha = "IA")
# download
cornyieldsall <- nassqs_yields(params)##
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 2%
|
|== | 3%
|
|=== | 4%
|
|=== | 5%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======== | 11%
|
|======== | 12%
|
|========= | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 19%
|
|============== | 20%
|
|============== | 21%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 22%
|
|================ | 23%
|
|================= | 24%
|
|================= | 25%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 29%
|
|===================== | 30%
|
|===================== | 31%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|============================== | 44%
|
|=============================== | 44%
|
|=============================== | 45%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|===================================== | 54%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 59%
|
|========================================== | 60%
|
|========================================== | 61%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================= | 65%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 69%
|
|================================================= | 70%
|
|================================================= | 71%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|=================================================== | 74%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|====================================================== | 78%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 87%
|
|============================================================= | 88%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 89%
|
|=============================================================== | 90%
|
|=============================================================== | 91%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================= | 94%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 97%
|
|==================================================================== | 98%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 99%
|
|======================================================================| 100%cornyieldsall$county_ansi <- as.numeric(cornyieldsall$county_ansi)
cornyieldsall$yield <- as.numeric(cornyieldsall$Value)
# clean and filter this dataset
cornyields <- select(cornyieldsall, county_ansi, county_name, yield, year) %>%
filter(!is.na(county_ansi) & !is.na(yield))
cornyields <- tibble(cornyields)7.2 Extract Winneshiek County corn yields, fit a linear time trend, make a plot. Is there a significant time trend?
winnecorn <- cornyields %>%
filter(county_ansi == "191")
cornlm <- lm(yield ~ year, data = winnecorn)
summary(cornlm) #P=1.77e-13 R^2= 0.755##
## Call:
## lm(formula = yield ~ year, data = winnecorn)
##
## Residuals:
## Min 1Q Median 3Q Max
## -51.163 -1.841 2.363 9.437 24.376
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4763.290 448.286 -10.63 4.46e-13 ***
## year 2.457 0.224 10.96 1.77e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 16.97 on 39 degrees of freedom
## Multiple R-squared: 0.7551, Adjusted R-squared: 0.7488
## F-statistic: 120.2 on 1 and 39 DF, p-value: 1.767e-13ggplot(winnecorn, mapping = aes(x = year, y = yield)) +
geom_point() +
theme_bw() +
labs(x = "Year", y = "Corn Yield") +
geom_smooth(method = lm, se=TRUE, color="#78917E", fill="#C5DDB3")## `geom_smooth()` using formula 'y ~ x'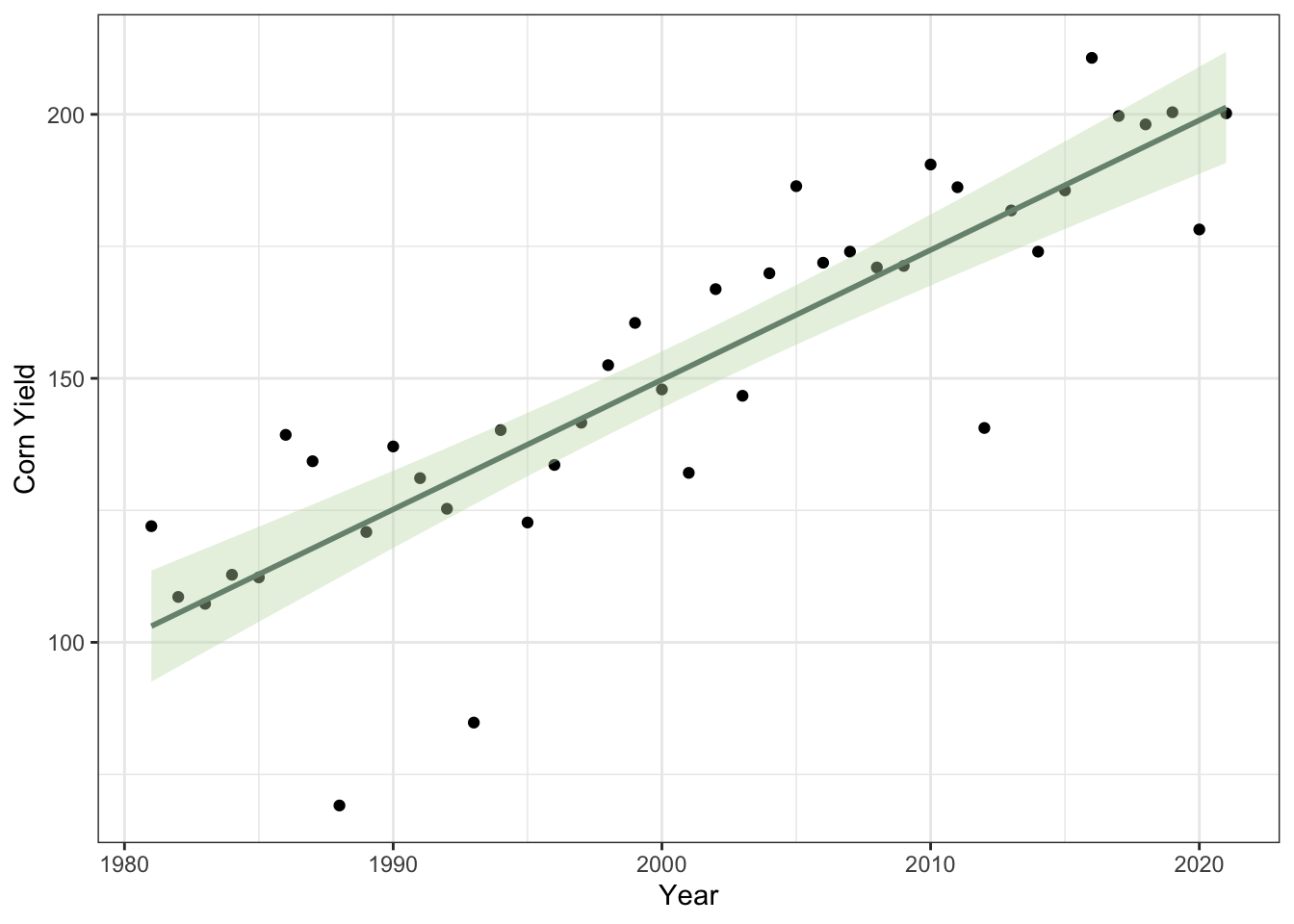
Figure 7.1: Linear regression of corn yields over time (years) in Winneshieck County, Iowa.
There is a significant positive correlation between corn yields and years in Winneshieck County, with an R-squared value of 0.755 and a P-value of 1.77e-13.
7.3 Fit a quadratic time trend (i.e., year + year^2) and make a plot. Is there evidence for slowing yield growth?
winnecorn$yearsq <- winnecorn$year^2 #square explanatory variables for quadratic
lm_cornquad <- lm(yield ~ year + yearsq, winnecorn)
summary(lm_cornquad)##
## Call:
## lm(formula = yield ~ year + yearsq, data = winnecorn)
##
## Residuals:
## Min 1Q Median 3Q Max
## -51.384 -3.115 1.388 9.743 25.324
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.583e+04 8.580e+04 0.301 0.765
## year -2.812e+01 8.576e+01 -0.328 0.745
## yearsq 7.641e-03 2.143e-02 0.357 0.723
##
## Residual standard error: 17.17 on 38 degrees of freedom
## Multiple R-squared: 0.7559, Adjusted R-squared: 0.7431
## F-statistic: 58.84 on 2 and 38 DF, p-value: 2.311e-12winnecorn$y_fitted <- lm_cornquad$fitted.values
#with the fitted values, create a non-linear trend
ggplot(winnecorn) +
geom_point(mapping = aes(x = year, y = yield)) +
geom_line(mapping = aes(x = year, y = y_fitted)) +
theme_bw() +
labs(x = "Year", y = "Corn Yield")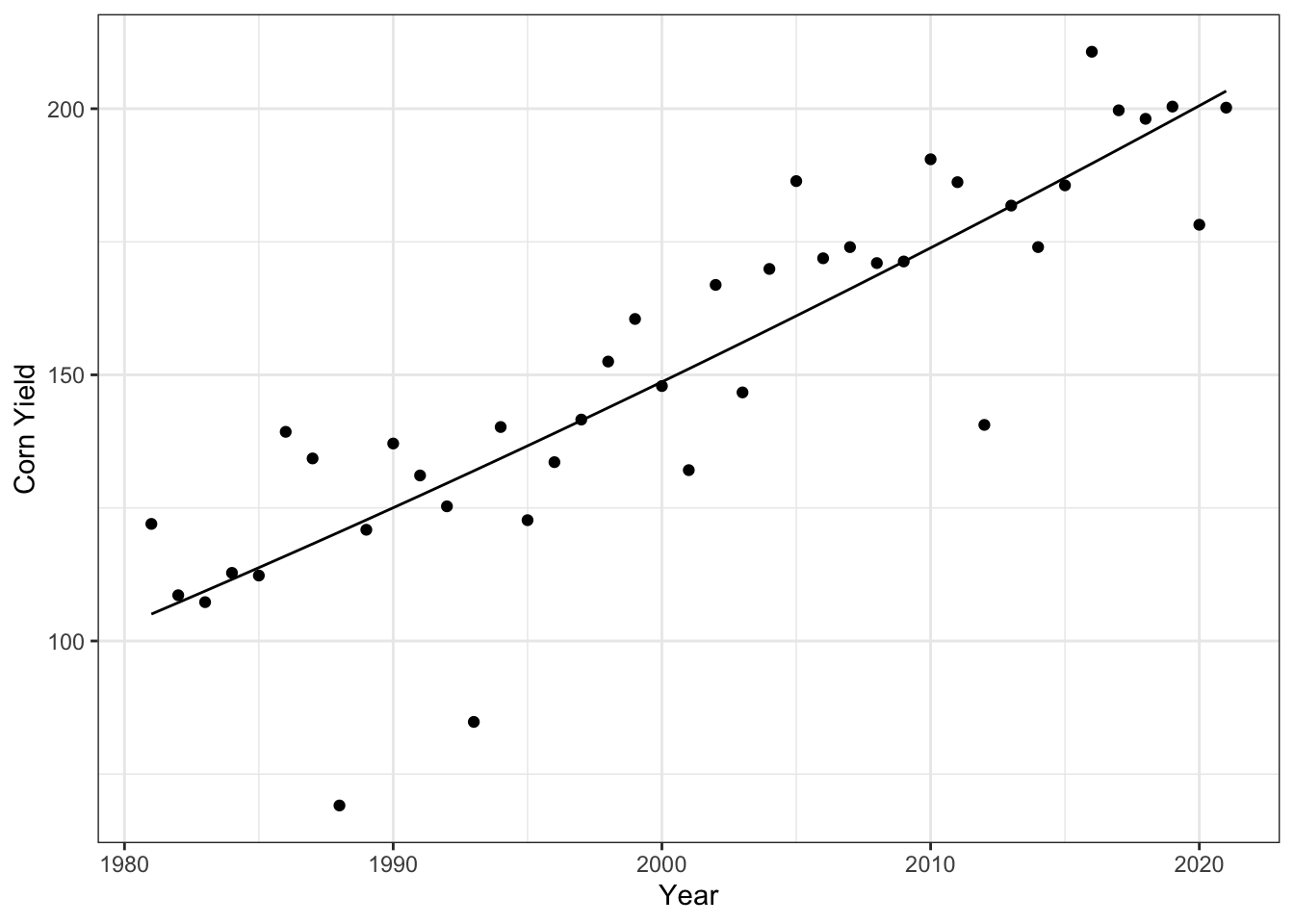
Figure 7.2: Quadratic fit of corn yields over time (years) in Winneshieck County, Iowa.
When we fit a quadratic line to the data, we find that it follows very closely to a linear regression, suggesting a fairly linear relationship between corn yields and years in Winneshieck County. There is no evidence of slowing yield growth in the model.
7.4 Time Series: Let’s analyze the relationship between temperature and yields for the Winneshiek County time series. Use data on yield and summer avg Tmax. Is adding year or Tmax^2 to your model helpful? Make a plot and interpret the results.
# Winneshiek County summer temp maxes
tmaxdf$doy <- as.numeric(tmaxdf$doy)
tmaxdf$year <- as.numeric(as.character(tmaxdf$year))
tmaxdf$tmax <- as.numeric(tmaxdf$tmax)
winnesummer <- tmaxdf %>%
filter(countyfp==191 & doy >= 152 & doy <= 243) %>% #day 152= June 1, 243= Aug 31
group_by(year) %>%
summarize(meantmax = mean(tmax))
lm_summertmax <- lm(meantmax ~ year, winnesummer)
summary(lm_summertmax) #not sig##
## Call:
## lm(formula = meantmax ~ year, data = winnesummer)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.5189 -0.7867 -0.0341 0.6859 3.7415
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 41.57670 36.44848 1.141 0.262
## year -0.00747 0.01823 -0.410 0.684
##
## Residual standard error: 1.232 on 36 degrees of freedom
## Multiple R-squared: 0.004644, Adjusted R-squared: -0.02301
## F-statistic: 0.168 on 1 and 36 DF, p-value: 0.6844winnesummer$yearsq <- winnesummer$year^2 #square explanatory variables for quadratic
winnesummer$tmaxsq <- winnesummer$meantmax^2
lm_summerquad <- lm(meantmax ~ year + yearsq, winnesummer)
summary(lm_summerquad)##
## Call:
## lm(formula = meantmax ~ year + yearsq, data = winnesummer)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.4617 -0.8812 -0.0530 0.7204 3.7308
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.618e+03 7.519e+03 0.481 0.633
## year -3.585e+00 7.521e+00 -0.477 0.637
## yearsq 8.946e-04 1.881e-03 0.476 0.637
##
## Residual standard error: 1.246 on 35 degrees of freedom
## Multiple R-squared: 0.01104, Adjusted R-squared: -0.04547
## F-statistic: 0.1953 on 2 and 35 DF, p-value: 0.8235winnesummer$t_fitted <- lm_summerquad$fitted.values
# Join yield and temp data
winne <- inner_join(winnecorn, winnesummer)## Joining, by = c("year", "yearsq")lmwinne <- lm(yield ~ yearsq + tmaxsq, data = winne)
summary(lmwinne)##
## Call:
## lm(formula = yield ~ yearsq + tmaxsq, data = winne)
##
## Residuals:
## Min 1Q Median 3Q Max
## -53.353 -7.496 2.089 9.806 27.874
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.314e+03 2.557e+02 -9.047 1.09e-10 ***
## yearsq 6.274e-04 6.295e-05 9.968 9.22e-12 ***
## tmaxsq -6.445e-02 4.245e-02 -1.518 0.138
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 16.97 on 35 degrees of freedom
## Multiple R-squared: 0.7492, Adjusted R-squared: 0.7349
## F-statistic: 52.28 on 2 and 35 DF, p-value: 3.074e-11winne$allfit <- lmwinne$fitted.values
ggplot(winne) +
geom_point(mapping = aes(x = year, y = yield)) +
geom_line(mapping = aes(x = year, y = allfit, color="red")) +
geom_line(mapping = aes(x = year, y = y_fitted, color="blue")) +
theme_bw() +
scale_colour_manual(name = "Model",
values =c("red"="red","blue"="blue"), labels = c("Fit with Max Temp and Year", "Quadratic Yield Fit")) +
labs(x = "Year", y = "Corn Yield")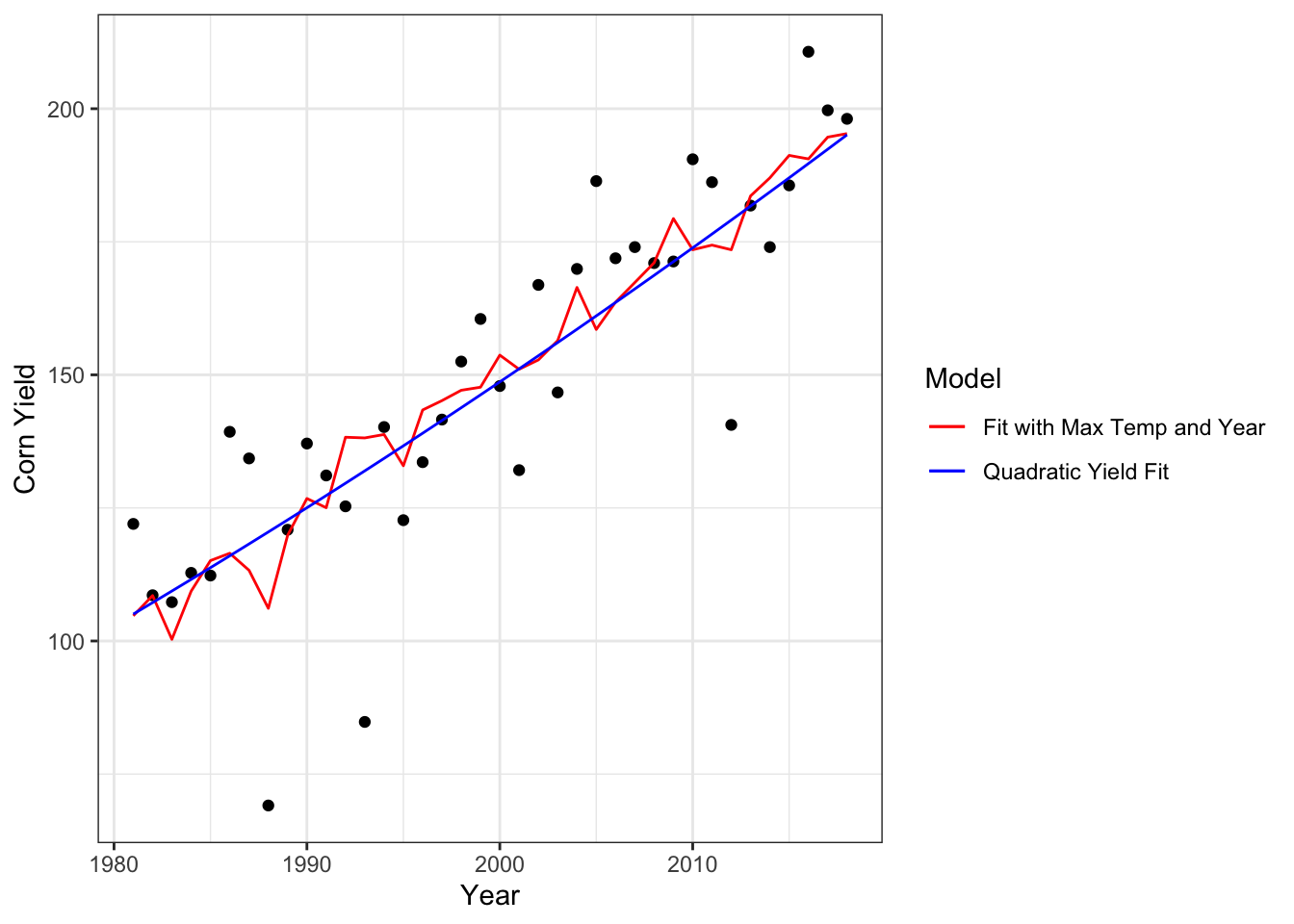
Figure 7.3: Comparative quadratic fit of corn yields over time (blue) and fitted line with maximum summer temperatures as well (red) in Winneshieck County, Iowa.
Adding maximum temperature trends to the model shows a similar trend, but peaks and dips in the fitted line highlight some of the outlying yield values and suggest an underlying relationship between maximum temperatures and yields. However, the relationship between squared maximum temperature and yield has a P-value of 0.14, compared with the year squared P-value of 9.22e-12, so it is clearly not the important driver of trends. This model has an R-squared value of 0.749, around the same as (slightly lower than) the simple linear regression model with only yield vs. year. Thus, adding temperature doesn’t significantly add to our understanding of yield trends in Winneshieck County.
7.5 Cross-Section: Analyze the relationship between temperature and yield across all counties in 2018. Is there a relationship? Interpret the results.
corn2018 <- cornyields %>%
filter(year == "2018") %>%
mutate_at(vars(county_ansi), funs(factor))
tmax2018 <- tmaxdf %>%
filter(year == "2018") %>%
filter(doy >= 152 & doy <= 243) %>%
group_by(countyfp) %>%
rename("county_ansi" = "countyfp") %>%
summarize(meantmax = mean(tmax))
yieldtemp_2018 <- inner_join(corn2018, tmax2018, by="county_ansi") %>%
mutate(tmaxsq = (meantmax^2))
yt_lm <- lm(yield ~ meantmax + tmaxsq, data = yieldtemp_2018)
summary(yt_lm)##
## Call:
## lm(formula = yield ~ meantmax + tmaxsq, data = yieldtemp_2018)
##
## Residuals:
## Min 1Q Median 3Q Max
## -44.221 -15.399 5.007 14.541 30.879
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5501.602 1860.830 -2.957 0.00397 **
## meantmax 406.789 131.493 3.094 0.00263 **
## tmaxsq -7.256 2.321 -3.126 0.00239 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 18.75 on 90 degrees of freedom
## Multiple R-squared: 0.1317, Adjusted R-squared: 0.1124
## F-statistic: 6.827 on 2 and 90 DF, p-value: 0.001736yieldtemp_2018$ytfit <- yt_lm$fitted.values
ggplot(yieldtemp_2018) +
geom_point(mapping = aes(x = meantmax, y = yield)) +
geom_line(mapping = aes(x = meantmax, y = ytfit, color="red")) +
theme_bw() + theme(legend.position="none") +
labs(x = "Mean Max Temperature (C)", y = "Corn Yield")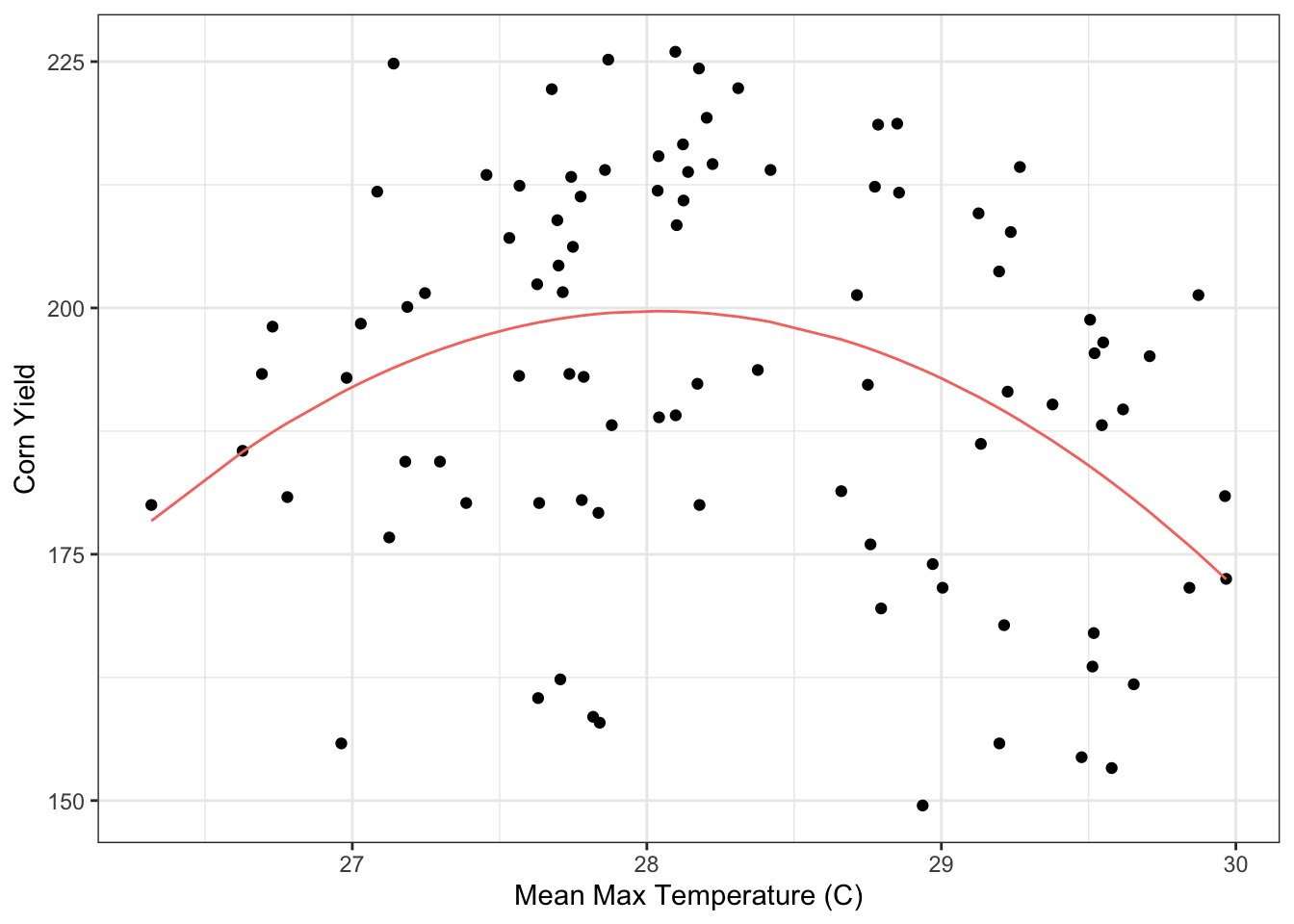
Figure 7.4: Quadratic fit of corn yields versus maximum summer temperatures (Degrees C) across Iowa.
There is a clear relationship with maximum temperatures and corn yields demonstrated in Figure 4. As we might expect, there appears to be a “sweet spot” in regard to temperature, with corn crops performing best at moderate temperatures and yields falling off at both low and high temperature years. Lower mean maximum temperatures may indicate even lower temperatures that can shock crops, and high means are likely to cause high evaporation and withering. P<0.003 for the relationship between temperature and corn yield across Iowa.
7.6 Panel: One way to leverage multiple time series is to group all data into what is called a “panel” regression.
Convert the county ID code (“countyfp” or “county_ansi”) into factor using as.factor, then include this variable in a regression using all counties’ yield and summer temperature data. How does the significance of your temperature coefficients (Tmax, Tmax^2) change? Make a plot comparing actual and fitted yields and interpret the results of your model.
corn_all <- cornyields %>%
mutate_at(vars(county_ansi), funs(factor))
tmax_all <- tmaxdf %>%
filter(doy >= 152 & doy <= 243) %>%
group_by(countyfp, year) %>%
rename("county_ansi" = "countyfp") %>%
summarize(meantmax = mean(tmax))## `summarise()` has grouped output by 'county_ansi'. You can override using the
## `.groups` argument.yieldtemp_all <- inner_join(corn_all, tmax_all) %>%
mutate(tmaxsq = (meantmax^2)) %>%
mutate(yearsq = year^2)## Joining, by = c("county_ansi", "year")ytc_lm <- lm(yield ~ year + meantmax + tmaxsq + county_ansi, data = yieldtemp_all)
summary(ytc_lm)##
## Call:
## lm(formula = yield ~ year + meantmax + tmaxsq + county_ansi,
## data = yieldtemp_all)
##
## Residuals:
## Min 1Q Median 3Q Max
## -81.645 -9.720 1.924 13.232 40.409
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.826e+03 9.804e+01 -59.431 < 2e-16 ***
## year 2.203e+00 2.836e-02 77.664 < 2e-16 ***
## meantmax 1.182e+02 6.108e+00 19.352 < 2e-16 ***
## tmaxsq -2.225e+00 1.085e-01 -20.503 < 2e-16 ***
## county_ansi3 -4.527e+00 4.321e+00 -1.048 0.294839
## county_ansi5 2.716e+00 4.343e+00 0.625 0.531743
## county_ansi7 -1.828e+01 4.350e+00 -4.203 2.70e-05 ***
## county_ansi9 5.068e+00 4.323e+00 1.172 0.241144
## county_ansi11 7.186e+00 4.325e+00 1.661 0.096732 .
## county_ansi13 7.289e+00 4.329e+00 1.684 0.092303 .
## county_ansi15 1.498e+01 4.323e+00 3.466 0.000534 ***
## county_ansi17 1.133e+01 4.332e+00 2.615 0.008966 **
## county_ansi19 7.651e+00 4.334e+00 1.765 0.077577 .
## county_ansi21 8.640e+00 4.328e+00 1.996 0.045974 *
## county_ansi23 9.089e+00 4.327e+00 2.100 0.035779 *
## county_ansi25 1.039e+01 4.326e+00 2.401 0.016400 *
## county_ansi27 9.666e+00 4.323e+00 2.236 0.025421 *
## county_ansi29 6.145e+00 4.321e+00 1.422 0.155092
## county_ansi31 1.579e+01 4.324e+00 3.651 0.000264 ***
## county_ansi33 4.582e+00 4.338e+00 1.056 0.290980
## county_ansi35 1.390e+01 4.325e+00 3.213 0.001325 **
## county_ansi37 2.169e+00 4.341e+00 0.500 0.617274
## county_ansi39 -2.404e+01 4.350e+00 -5.527 3.48e-08 ***
## county_ansi41 6.611e+00 4.329e+00 1.527 0.126809
## county_ansi43 8.864e+00 4.337e+00 2.044 0.041033 *
## county_ansi45 1.055e+01 4.325e+00 2.439 0.014756 *
## county_ansi47 6.528e+00 4.324e+00 1.510 0.131221
## county_ansi49 1.081e+01 4.321e+00 2.502 0.012386 *
## county_ansi51 -1.457e+01 4.352e+00 -3.349 0.000820 ***
## county_ansi53 -1.603e+01 4.350e+00 -3.686 0.000232 ***
## county_ansi55 9.423e+00 4.338e+00 2.172 0.029916 *
## county_ansi57 1.050e+01 4.321e+00 2.429 0.015186 *
## county_ansi59 2.906e+00 4.336e+00 0.670 0.502836
## county_ansi61 9.795e+00 4.340e+00 2.257 0.024059 *
## county_ansi63 7.232e+00 4.340e+00 1.666 0.095754 .
## county_ansi65 7.319e+00 4.341e+00 1.686 0.091905 .
## county_ansi67 4.791e+00 4.334e+00 1.106 0.269008
## county_ansi69 1.131e+01 4.330e+00 2.612 0.009035 **
## county_ansi71 1.358e+01 4.330e+00 3.136 0.001726 **
## county_ansi73 1.462e+01 4.321e+00 3.382 0.000727 ***
## county_ansi75 1.151e+01 4.328e+00 2.659 0.007863 **
## county_ansi77 3.379e+00 4.321e+00 0.782 0.434297
## county_ansi79 1.315e+01 4.324e+00 3.042 0.002370 **
## county_ansi81 8.706e+00 4.340e+00 2.006 0.044917 *
## county_ansi83 1.395e+01 4.326e+00 3.225 0.001271 **
## county_ansi85 6.891e+00 4.321e+00 1.595 0.110834
## county_ansi87 5.280e+00 4.321e+00 1.222 0.221864
## county_ansi89 9.433e-01 4.364e+00 0.216 0.828875
## county_ansi91 9.881e+00 4.334e+00 2.280 0.022661 *
## county_ansi93 1.186e+01 4.325e+00 2.743 0.006124 **
## county_ansi95 7.214e+00 4.322e+00 1.669 0.095161 .
## county_ansi97 -1.386e+00 4.330e+00 -0.320 0.748823
## county_ansi99 1.440e+01 4.322e+00 3.332 0.000871 ***
## county_ansi101 5.352e-01 4.325e+00 0.124 0.901510
## county_ansi103 4.380e+00 4.322e+00 1.013 0.310971
## county_ansi105 7.730e+00 4.328e+00 1.786 0.074158 .
## county_ansi107 2.203e+00 4.321e+00 0.510 0.610224
## county_ansi109 1.222e+01 4.335e+00 2.819 0.004839 **
## county_ansi111 1.779e+00 4.324e+00 0.411 0.680740
## county_ansi113 6.415e+00 4.326e+00 1.483 0.138218
## county_ansi115 7.330e+00 4.322e+00 1.696 0.089966 .
## county_ansi117 -2.168e+01 4.381e+00 -4.949 7.81e-07 ***
## county_ansi119 9.328e+00 4.325e+00 2.157 0.031063 *
## county_ansi121 -2.587e+00 4.321e+00 -0.599 0.549390
## county_ansi123 8.152e+00 4.321e+00 1.887 0.059302 .
## county_ansi125 1.919e+00 4.321e+00 0.444 0.656948
## county_ansi127 1.418e+01 4.326e+00 3.278 0.001055 **
## county_ansi129 1.023e+01 4.385e+00 2.332 0.019741 *
## county_ansi131 7.285e+00 4.352e+00 1.674 0.094242 .
## county_ansi133 7.987e-01 4.321e+00 0.185 0.853378
## county_ansi135 -1.585e+01 4.350e+00 -3.643 0.000273 ***
## county_ansi137 5.885e+00 4.322e+00 1.362 0.173381
## county_ansi139 8.283e+00 4.321e+00 1.917 0.055337 .
## county_ansi141 1.423e+01 4.328e+00 3.288 0.001018 **
## county_ansi143 8.743e+00 4.337e+00 2.016 0.043890 *
## county_ansi145 -3.674e-01 4.322e+00 -0.085 0.932261
## county_ansi147 7.261e+00 4.330e+00 1.677 0.093601 .
## county_ansi149 7.352e+00 4.322e+00 1.701 0.089007 .
## county_ansi151 1.150e+01 4.326e+00 2.659 0.007880 **
## county_ansi153 1.403e+01 4.321e+00 3.247 0.001178 **
## county_ansi155 1.127e+01 4.350e+00 2.590 0.009627 **
## county_ansi157 1.055e+01 4.322e+00 2.441 0.014702 *
## county_ansi159 -2.070e+01 4.321e+00 -4.792 1.72e-06 ***
## county_ansi161 9.390e+00 4.326e+00 2.170 0.030050 *
## county_ansi163 1.628e+01 4.323e+00 3.765 0.000169 ***
## county_ansi165 7.673e+00 4.323e+00 1.775 0.075966 .
## county_ansi167 1.558e+01 4.323e+00 3.603 0.000318 ***
## county_ansi169 1.122e+01 4.325e+00 2.593 0.009543 **
## county_ansi171 9.740e+00 4.325e+00 2.252 0.024387 *
## county_ansi173 -1.404e+01 4.350e+00 -3.228 0.001256 **
## county_ansi175 -1.155e+01 4.350e+00 -2.655 0.007967 **
## county_ansi177 -5.278e+00 4.329e+00 -1.219 0.222881
## county_ansi179 -3.220e+00 4.351e+00 -0.740 0.459267
## county_ansi181 -2.159e+00 4.321e+00 -0.500 0.617309
## county_ansi183 1.042e+01 4.321e+00 2.410 0.015981 *
## county_ansi185 -2.189e+01 4.350e+00 -5.033 5.07e-07 ***
## county_ansi187 1.421e+01 4.326e+00 3.285 0.001029 **
## county_ansi189 8.236e+00 4.344e+00 1.896 0.058035 .
## county_ansi191 4.567e+00 4.350e+00 1.050 0.293826
## county_ansi193 2.799e+00 4.321e+00 0.648 0.517252
## county_ansi195 6.123e+00 4.356e+00 1.406 0.159892
## county_ansi197 1.156e+01 4.329e+00 2.669 0.007634 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 18.83 on 3646 degrees of freedom
## Multiple R-squared: 0.7207, Adjusted R-squared: 0.7129
## F-statistic: 93.13 on 101 and 3646 DF, p-value: < 2.2e-16yieldtemp_all$fittedyield <- ytc_lm$fitted.values
ggplot(yieldtemp_all, mapping = aes(x = fittedyield, y = yield)) +
geom_point() +
geom_smooth(method="lm") +
theme_bw() + theme(legend.position="none") +
labs(x = "Fitted Yield", y = "Actual Yield")## `geom_smooth()` using formula 'y ~ x'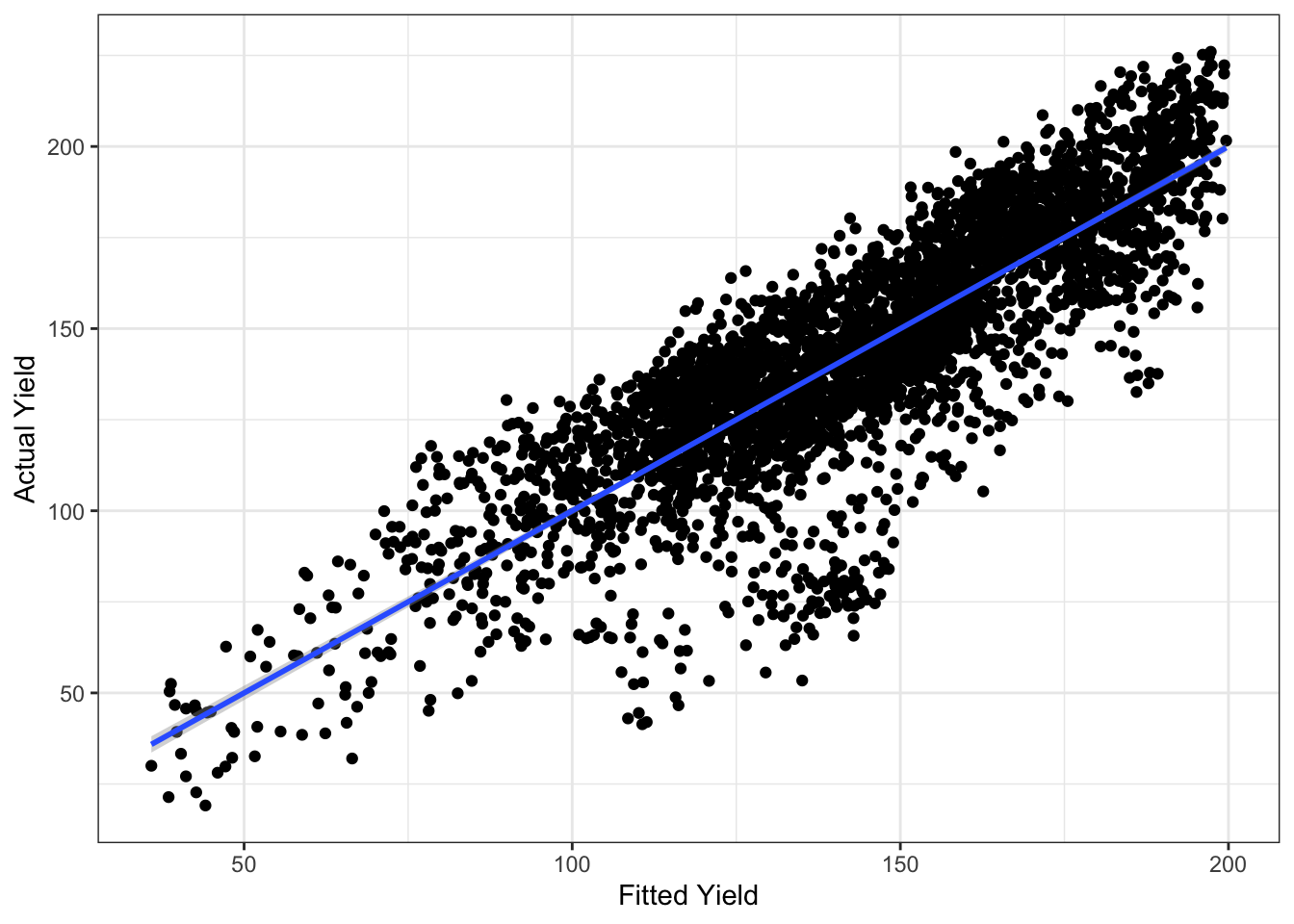
Figure 7.5: Fitted model yield values versus actual yield values for all counties of Iowa over all available years, from 1981 to 2018.
par(mfrow=c(2,2))
plot(ytc_lm)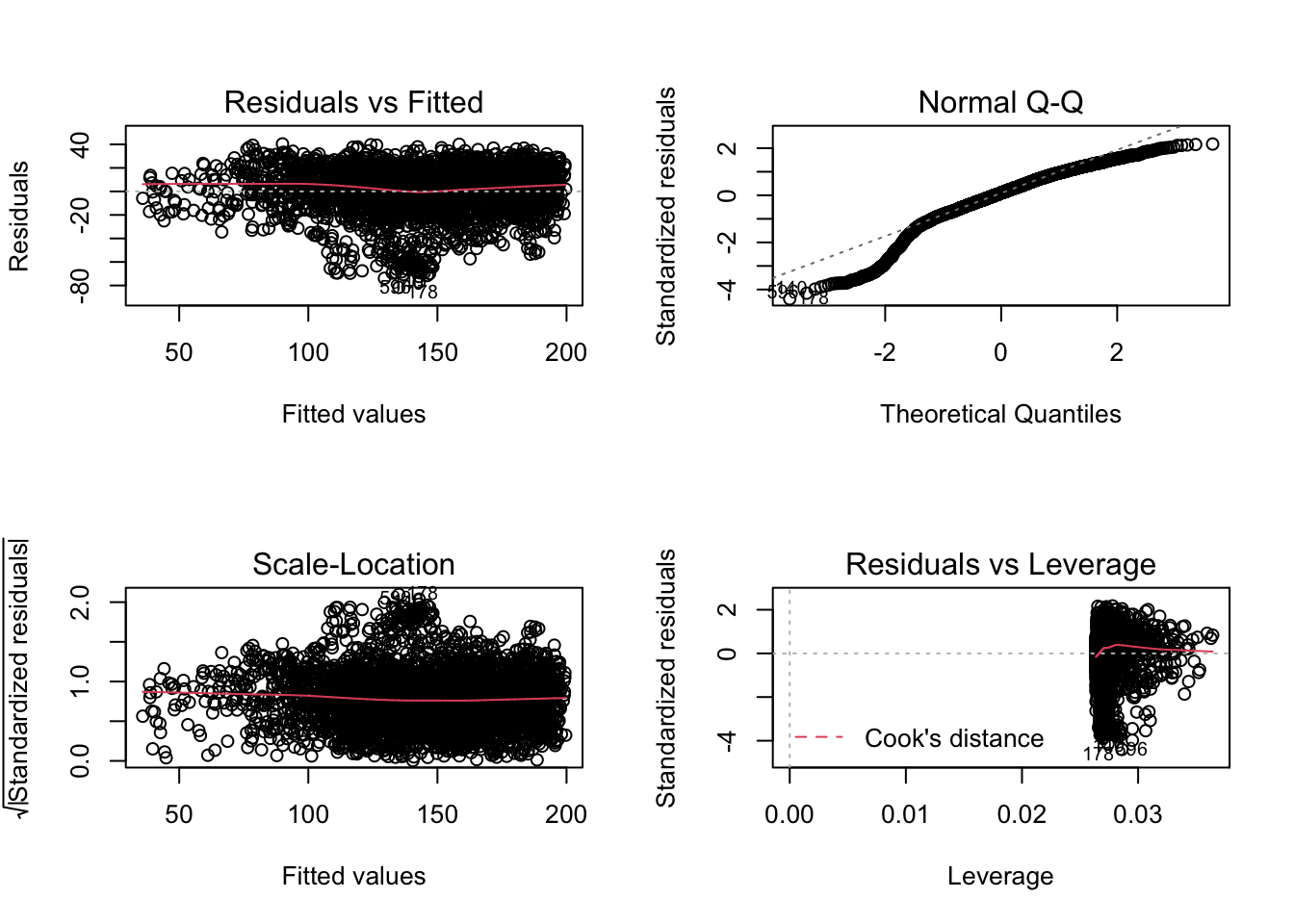
Figure 7.6: Residuals (top left), Normal Q-Q (top right), Scale-Location (bottom left), and Cook’s Distance (bottom right) plots for the panel regression model.
As a panel regression of all counties over all years, the statistical significance of year, mean maximum temperature, and squared maximum temperature as predictors of yield becomes stronger (P<2e-16 for each). The R squared value for the model is 0.721, indicating a pretty good fit, as is evident in Figure 5. However, the residuals for the model are pretty wide (Figures 5, 6) and the data may not be very normally distributed (Figure 6).
7.7 Soybeans: Download NASS data on soybean yields and explore either a time series relationship for a given county, the cross-sectional relationship for a given year, or a panel across all counties and years.
# parameters to query on
params2 <- list(commodity_desc = "SOYBEANS", prodn_practice_desc = "ALL PRODUCTION PRACTICES", year__GE = 1981, state_alpha = "IA")
# download
soyyieldsall <- nassqs_yields(params)##
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 2%
|
|== | 3%
|
|=== | 4%
|
|=== | 5%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 9%
|
|======= | 10%
|
|======= | 11%
|
|======== | 11%
|
|======== | 12%
|
|========= | 12%
|
|========= | 13%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 19%
|
|============== | 20%
|
|============== | 21%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 22%
|
|================ | 23%
|
|================= | 24%
|
|================= | 25%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 29%
|
|===================== | 30%
|
|===================== | 31%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|============================== | 44%
|
|=============================== | 44%
|
|=============================== | 45%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 49%
|
|=================================== | 50%
|
|=================================== | 51%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|===================================== | 54%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 59%
|
|========================================== | 60%
|
|========================================== | 61%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================= | 65%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 69%
|
|================================================= | 70%
|
|================================================= | 71%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|=================================================== | 74%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|====================================================== | 78%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|======================================================== | 81%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 86%
|
|============================================================= | 87%
|
|============================================================= | 88%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 89%
|
|=============================================================== | 90%
|
|=============================================================== | 91%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 97%
|
|==================================================================== | 98%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 99%
|
|======================================================================| 100%soyyieldsall$county_ansi <- as.numeric(soyyieldsall$county_ansi)
soyyieldsall$yield <- as.numeric(soyyieldsall$Value)
# clean and filter this dataset
soy <- select(soyyieldsall, county_ansi, county_name, yield, year) %>%
filter(!is.na(county_ansi) & !is.na(yield))
soy <- tibble(soy)
soy_panel <- soy %>%
mutate_at(vars(county_ansi), funs(factor)) %>%
mutate(yearsq = year^2)
soypanel_lm <- lm(yield ~ year + yearsq + county_ansi, data = soy_panel)
summary(soypanel_lm)##
## Call:
## lm(formula = yield ~ year + yearsq + county_ansi, data = soy_panel)
##
## Residuals:
## Min 1Q Median 3Q Max
## -100.865 -9.428 3.328 14.357 54.326
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.646e+04 1.090e+04 4.263 2.06e-05 ***
## year -4.859e+01 1.089e+01 -4.461 8.38e-06 ***
## yearsq 1.272e-02 2.722e-03 4.672 3.09e-06 ***
## county_ansi3 -3.974e+00 4.809e+00 -0.826 0.408591
## county_ansi5 1.128e+01 4.749e+00 2.376 0.017550 *
## county_ansi7 -1.878e+01 4.778e+00 -3.931 8.61e-05 ***
## county_ansi9 9.877e+00 4.749e+00 2.080 0.037621 *
## county_ansi11 1.206e+01 4.749e+00 2.539 0.011162 *
## county_ansi13 1.391e+01 4.749e+00 2.930 0.003413 **
## county_ansi15 1.785e+01 4.749e+00 3.759 0.000173 ***
## county_ansi17 1.899e+01 4.749e+00 3.998 6.50e-05 ***
## county_ansi19 1.609e+01 4.749e+00 3.389 0.000709 ***
## county_ansi21 1.519e+01 4.749e+00 3.198 0.001396 **
## county_ansi23 1.612e+01 4.749e+00 3.394 0.000696 ***
## county_ansi25 1.603e+01 4.749e+00 3.375 0.000744 ***
## county_ansi27 1.435e+01 4.749e+00 3.023 0.002523 **
## county_ansi29 7.386e+00 4.749e+00 1.555 0.119953
## county_ansi31 1.942e+01 4.749e+00 4.088 4.43e-05 ***
## county_ansi33 1.250e+01 4.749e+00 2.632 0.008515 **
## county_ansi35 1.961e+01 4.778e+00 4.105 4.13e-05 ***
## county_ansi37 1.127e+01 4.749e+00 2.373 0.017672 *
## county_ansi39 -2.380e+01 4.841e+00 -4.916 9.19e-07 ***
## county_ansi41 1.302e+01 4.749e+00 2.742 0.006141 **
## county_ansi43 1.659e+01 4.749e+00 3.493 0.000483 ***
## county_ansi45 1.556e+01 4.749e+00 3.276 0.001061 **
## county_ansi47 1.300e+01 4.749e+00 2.737 0.006228 **
## county_ansi49 1.131e+01 4.749e+00 2.382 0.017259 *
## county_ansi51 -1.838e+01 4.778e+00 -3.847 0.000121 ***
## county_ansi53 -1.681e+01 4.841e+00 -3.472 0.000521 ***
## county_ansi55 1.775e+01 4.749e+00 3.738 0.000188 ***
## county_ansi57 9.205e+00 4.778e+00 1.926 0.054127 .
## county_ansi59 9.501e+00 4.749e+00 2.001 0.045507 *
## county_ansi61 1.838e+01 4.749e+00 3.871 0.000110 ***
## county_ansi63 1.503e+01 4.778e+00 3.145 0.001676 **
## county_ansi65 1.555e+01 4.749e+00 3.275 0.001065 **
## county_ansi67 1.283e+01 4.749e+00 2.702 0.006920 **
## county_ansi69 1.810e+01 4.749e+00 3.810 0.000141 ***
## county_ansi71 5.259e+00 4.778e+00 1.100 0.271183
## county_ansi73 1.644e+01 4.749e+00 3.461 0.000545 ***
## county_ansi75 1.853e+01 4.749e+00 3.901 9.75e-05 ***
## county_ansi77 5.347e+00 4.749e+00 1.126 0.260249
## county_ansi79 1.771e+01 4.778e+00 3.706 0.000214 ***
## county_ansi81 1.716e+01 4.749e+00 3.614 0.000306 ***
## county_ansi83 1.836e+01 4.749e+00 3.866 0.000112 ***
## county_ansi85 6.372e+00 4.809e+00 1.325 0.185252
## county_ansi87 2.204e+00 4.749e+00 0.464 0.642690
## county_ansi89 9.845e+00 4.749e+00 2.073 0.038239 *
## county_ansi91 1.758e+01 4.749e+00 3.703 0.000216 ***
## county_ansi93 1.808e+01 4.778e+00 3.784 0.000156 ***
## county_ansi95 9.245e+00 4.778e+00 1.935 0.053090 .
## county_ansi97 5.382e+00 4.749e+00 1.133 0.257218
## county_ansi99 1.823e+01 4.778e+00 3.815 0.000138 ***
## county_ansi101 -6.065e+00 4.749e+00 -1.277 0.201671
## county_ansi103 6.598e+00 4.778e+00 1.381 0.167447
## county_ansi105 1.373e+01 4.778e+00 2.874 0.004069 **
## county_ansi107 1.030e+00 4.749e+00 0.217 0.828258
## county_ansi109 1.968e+01 4.749e+00 4.145 3.47e-05 ***
## county_ansi111 -4.248e+00 4.749e+00 -0.894 0.371157
## county_ansi113 1.244e+01 4.778e+00 2.604 0.009251 **
## county_ansi115 4.608e+00 4.749e+00 0.970 0.331929
## county_ansi117 -2.150e+01 4.841e+00 -4.441 9.20e-06 ***
## county_ansi119 1.472e+01 4.749e+00 3.100 0.001952 **
## county_ansi121 -1.277e+00 4.749e+00 -0.269 0.788032
## county_ansi123 8.308e+00 4.749e+00 1.749 0.080294 .
## county_ansi125 1.995e+00 4.778e+00 0.418 0.676297
## county_ansi127 2.112e+01 4.778e+00 4.419 1.02e-05 ***
## county_ansi129 5.192e+00 4.809e+00 1.080 0.280353
## county_ansi131 1.591e+01 4.749e+00 3.349 0.000818 ***
## county_ansi133 1.767e-01 4.749e+00 0.037 0.970326
## county_ansi135 -1.612e+01 4.778e+00 -3.373 0.000751 ***
## county_ansi137 4.108e+00 4.749e+00 0.865 0.387051
## county_ansi139 8.369e+00 4.749e+00 1.762 0.078100 .
## county_ansi141 2.129e+01 4.749e+00 4.483 7.57e-06 ***
## county_ansi143 1.615e+01 4.749e+00 3.400 0.000680 ***
## county_ansi145 -2.245e+00 4.749e+00 -0.473 0.636402
## county_ansi147 1.413e+01 4.749e+00 2.975 0.002950 **
## county_ansi149 1.129e+01 4.778e+00 2.362 0.018212 *
## county_ansi151 1.801e+01 4.778e+00 3.770 0.000166 ***
## county_ansi153 1.401e+01 4.749e+00 2.949 0.003206 **
## county_ansi155 1.124e+01 4.778e+00 2.352 0.018734 *
## county_ansi157 1.181e+01 4.749e+00 2.487 0.012908 *
## county_ansi159 -2.035e+01 4.778e+00 -4.258 2.11e-05 ***
## county_ansi161 1.602e+01 4.749e+00 3.373 0.000751 ***
## county_ansi163 1.991e+01 4.749e+00 4.192 2.83e-05 ***
## county_ansi165 1.242e+01 4.778e+00 2.599 0.009393 **
## county_ansi167 2.019e+01 4.749e+00 4.252 2.17e-05 ***
## county_ansi169 1.555e+01 4.749e+00 3.275 0.001067 **
## county_ansi171 1.451e+01 4.749e+00 3.055 0.002266 **
## county_ansi173 -1.499e+01 4.778e+00 -3.137 0.001720 **
## county_ansi175 -1.023e+01 4.778e+00 -2.142 0.032273 *
## county_ansi177 -1.466e+01 4.749e+00 -3.086 0.002041 **
## county_ansi179 -5.652e+00 4.778e+00 -1.183 0.236907
## county_ansi181 -2.277e+00 4.809e+00 -0.473 0.635891
## county_ansi183 8.595e+00 4.778e+00 1.799 0.072137 .
## county_ansi185 -2.086e+01 4.778e+00 -4.365 1.30e-05 ***
## county_ansi187 2.017e+01 4.749e+00 4.247 2.21e-05 ***
## county_ansi189 1.687e+01 4.749e+00 3.552 0.000387 ***
## county_ansi191 1.306e+01 4.749e+00 2.750 0.005980 **
## county_ansi193 6.472e+00 4.749e+00 1.363 0.173049
## county_ansi195 1.503e+01 4.749e+00 3.164 0.001566 **
## county_ansi197 1.807e+01 4.749e+00 3.805 0.000144 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.37 on 3914 degrees of freedom
## Multiple R-squared: 0.6598, Adjusted R-squared: 0.6511
## F-statistic: 75.91 on 100 and 3914 DF, p-value: < 2.2e-16soy_panel$fittedyield <- soypanel_lm$fitted.values
ggplot(soy_panel, mapping = aes(x = year, y = yield)) +
geom_point() +
geom_line(mapping = aes(x = year, y = fittedyield, color="red")) +
geom_smooth(method="lm") +
theme_bw() + theme(legend.position="none") +
labs(x = "Year", y = "Soy Yield")## `geom_smooth()` using formula 'y ~ x'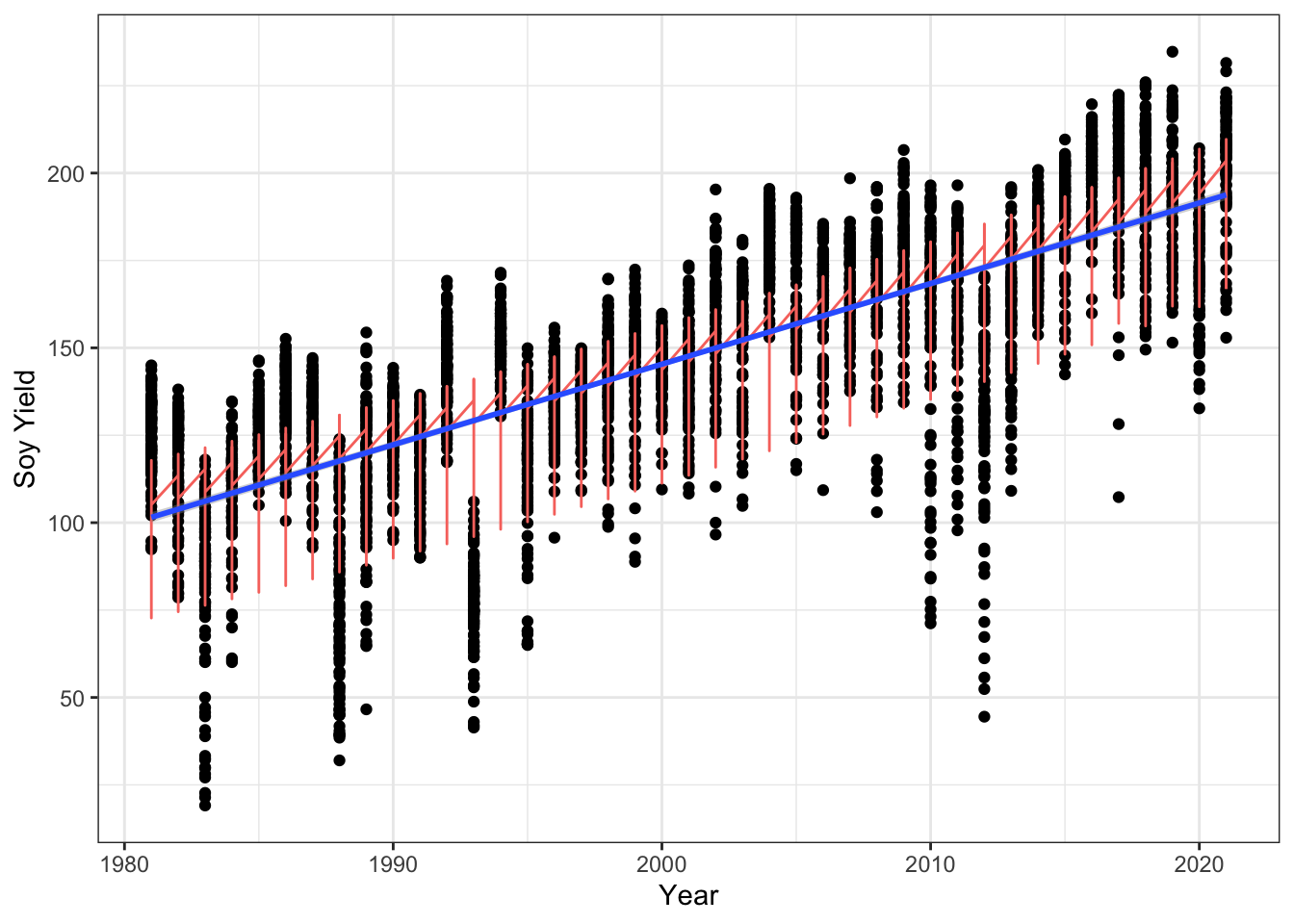
Figure 7.7: Soy yields over time (years) across all counties of Iowa, with a panel fit (orange), and linear fit (blue). Panel regression R squared is 0.660, with p<8.5e-06 for year and years squared versus yield.
Like with corn yields, soy yields in Iowa follow an upward trend over time, though with wide residuals (Figure 7).
7.8 Bonus: Find a package to make a county map of Iowa displaying some sort of information about yields or weather. Interpret your map.
library(sf) #Spatial package that can read and create shapefiles
library(mapview) #Interactive maps
library(USAboundaries) #USA states and counties
counties <- us_counties
Iowa_ct <- counties(states = 'iowa')
#str(Iowa_ct)
#mapview(Iowa_ct)
summer2018 <- tmaxdf %>%
filter(doy >= 152 & doy <= 243, year==2018) %>% #day 152= June 1, 243= Aug 31
group_by(countyfp, year) %>%
summarize(meantmax = mean(tmax))## `summarise()` has grouped output by 'countyfp'. You can override using the
## `.groups` argument.Itemp_2018 <- merge(Iowa_ct, summer2018)
mapview(Itemp_2018, zcol ='meantmax', col.regions=brewer.pal(9, "OrRd"), layer.name = "Mean Max. Summer Temp. (C)")